Subdivision pattern

Each subdivision of triangular or quadrilateral macro elements is based on a pattern. Regular patterns subdivide opposite edges with the same number of segments, as is shown in the following figure:

For irregular patterns at least 2 opposite edges have a different number of segments. This way a mesh refinement is achieved into one or two directions. A 2 digit ID distinguishes the patterns for regular and a 3 digit ID for irregular subdivisions. The pattern ID for regular subdivisions is 20 for macro elements 20-25, 30 for macro elements 30-35,60-65 and 40 for macro elements 40-45,80-85.

Besides the pattern ID the number of intermediate nodes for the edges of the macro element must be given.

With some patterns also a quotient q for the length of last to first FE edge can be given. The length of FE edges increases linearly for q > 1 and decreases linearly for q < 1.

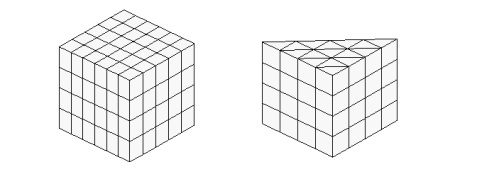
In case of solid elements a pattern is always applied to the bottom and the top surface. The direction perpendicular to the bottom surface will always be regularly subdivided, for this direction, the number of intermediate nodes and optionally a quotient for last to first FE edge length must be given.

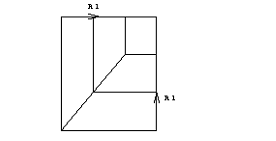
Following m1,m2,m3,m4 are the number of intermediate nodes for edges 1-4 of a quadrilateral macro element, where the edges are numbered counter clock wise beginning with the first element node. Direction R1 points from first to second node and direction R2 from second to third node.

With a regular pattern only values for m1 and m2 must be given, m3 = m1 and m4 = m2 are set automatically. Also quotients q1 and q2 for the two main directions of a quadrilateral macro element may be given.

With an irregular pattern the last two digits of the pattern ID define the subdivision pattern as shown in the following pictures. The first digit of the pattern ID determines the rotation of the pattern. The pattern is first applied to an unit element and is then mapped to the geometry of the macro element, where the first digit of the pattern ID gives the node of the macro element that coincides to the first node of the unit element.

Following pictures show the different subdivision patterns.

Pattern 101, 102, 104, 105

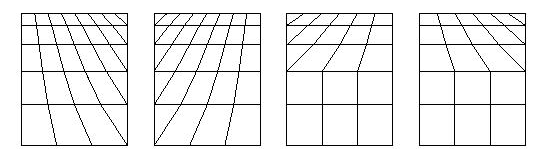
With pattern 101 and 102 a linear increase of the number of intermediate nodes is applied for direction R1 towards direction R2. The number of intermediate nodes for edge 1 (m1) and edge 2 (m2) must be given, m3 = m1+m2+1 and m4 = m2 are set.

With patterns 104 and 105 also m3 must be given, with abs(m3-m1) < m2. The smaller number of intermediate nodes will at first be constant in the direction of R2 and then linearly increased.

For direction R2 a quotient q for last to first FE edge length may be given.

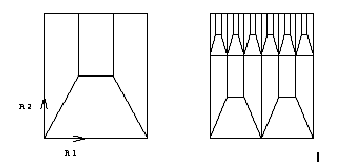
Pattern 121

A base pattern which subdivides a quadrilateral element into 4 FE elements as shown in the left following picture is lined up in direction R1 and R2. The number of intermediate nodes m1 and m2 for direction R1 and R2 must be given, m4 = m2 and m3 = (m1+1)*(3**(m2+1))-1 is set.

For direction R2 a quotient q for last to first FE edge length may be given.

Pattern 122

This pattern allows refinements in 2 directions by giving the subdivision parameters m1 and q1.

Pattern 123, 124, 125, 126

Pattern 123 does refinements in direction R2. m1,m2,m3 must be given, m4 = m3 is set, m1 must be odd, for m3 the condition m3 = (m1+1)*(2**n)-1 with n <= m2+1 must be met. For direction R2 a quotient q for last to first FE edge length may be given.

For pattern 124 m1 and m2 must be given, m3 = m1 and m4 = m2 are set.

For pattern 125 and 126 m1 and m2 must be given, m3 = 2*m1+1 and m4 = 2*m2+1 are set.

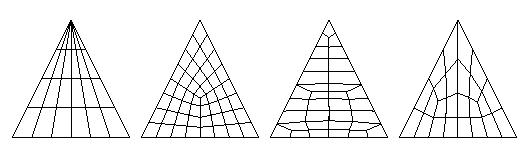
Pattern 133, 134, 135, 136

These are patterns for triangular macro elements, where m3 = m2.

With pattern 134 all edges are equally subdivided (m1 = m2 = m3) where m1 must be odd.

With Pattern 135 m1 must be odd and at least 1 and m2 must be at least 3 where m1 and m2 are independent of each other.

Pattern 136 is built upon 2 triangles by using pattern 134. m1 must be at least 3. Correlation between m1 and m2 is given by m1 = 2*m2+1 where m2 must be odd. Only m1 must be specified, m2, m3 are automatically set to m3 = m2 = (m1-1)/2. Pattern 136 especially may be useful when subdividing a semicircle area modeled by elements of type 32 into quadrilateral elements.

Pattern 134 is the default when subdividing macro elements of type 30-35, 60-65

Pattern 142

This pattern allows specifying independent numbers of intermediate nodes for all edges of the underlying macro element. If the sum of all intermediate nodes on edges is even for quadrilateral elements or odd for triangular elements, exclusively quadrilateral elements are generated. In the other cases one additional triangular element is generated.

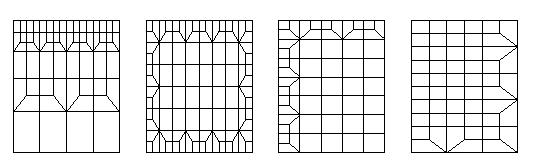
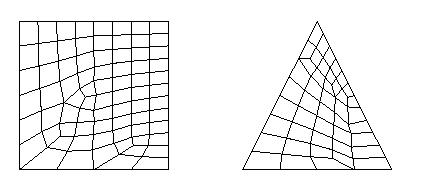
Pattern 150 for triangular and quadrilateral macro elements with curved edges

As with pattern 142 the number of intermediate nodes may be different for all edges. But with ID 150 the geometry of the macro element is taken into account for the definition of the pattern. The macro element is projected on a plane defined by the three first corner nodes of the macro element. The triangular or quadrilateral element in this plane is than subdivided using the algorithm described below for element type 400. This net is then mapped to an unit element and this pattern is further mapped to the geometry of the given macro element. The condition must be met, that the quotient of greatest to smallest FE edge length is not greater than 4.

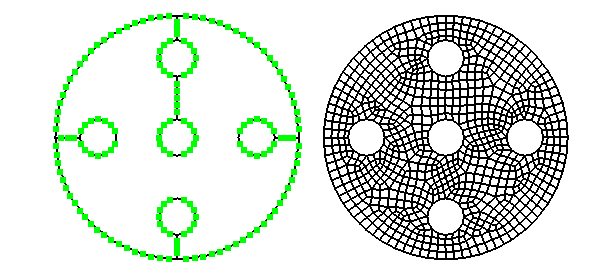
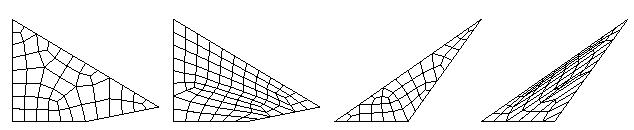
Pattern 150 should be used instead of pattern 142 when the angle of some corners of the macro element differ greatly from 90 degree. Following pictures show the differences of pattern 150 (left) and pattern 142 (right) for a quadrilateral and a triangular element.

Pattern for element type 105

Macro element type 105 is a planar element with up to 10 edges consisting of straight lines, circular arcs or spline curves. For each edge the subdivision must explicitly be specified using the commands Division or Pattern. With Pattern the following subdivision patterns can be applied.

Pattern 150

This invokes a free mesh generation as with element type 400 (see below).

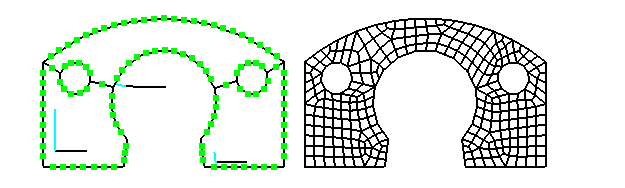
Pattern 40 or 142

These patterns can be used if 4 vertices of the polygon can be identified as corner nodes of a quadrilateral element. The first vertex of the polygon is always the first corner of the quadrilateral element. The remaining 3 corner nodes can be specified using the command Element definition and will be saved after the elements height. If no corner nodes are specified these vertices of the polygon are automatically selected which give the smallest inner angles.

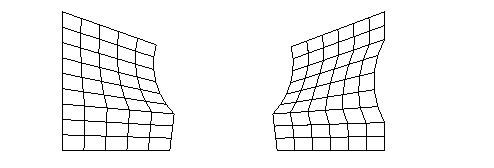
Pattern 151 - 551:

These pattern IDs can be used with macro elements of type 105 with 5 edges. At first, the element is divided into two quadrilateral elements by a line from a corner of the polygon to the middle of the opposite edge. The two resulting quadrilateral elements are divided by using the pattern 142. The first digit of the pattern ID tells, which vertex of the polygon is used for the division into two quadrilateral elements. Following picture shows pattern 151 and 251 if lower left vertex is the first element node.

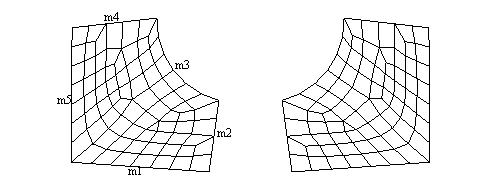
Pattern 152-552:

The pattern corresponds to pattern 151-551 with the difference that conditions for subdividing the edges 3 and 4 must be so that a regular subdivision with quadrilateral elements can be achieved. These conditions are: m4 = m2 and m3 = m1 + m5 + 1; m4 and m3 are corrected if they don’t meet this condition. The first digit specifies which vertex will be the starting vertex for subdivision into 2 quadrilateral elements. Following picture shows pattern 152 and 252 (see also demo “pattern15x.dem”).

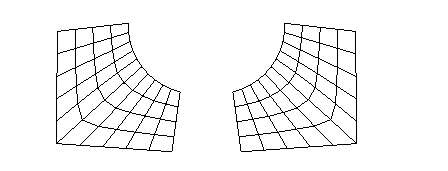
Pattern 161-661:

This pattern corresponds to pattern 151-551. It can be used for elements with 6 edges. The element is first subdivided into three quadrilateral elements, which are then subdivided by pattern 142. The first digit of the pattern ID tells which vertex of the polygon will be the starting vertex for division into three quadrilateral elements. Following picture shows pattern 161 and 561 if the lower left vertex is the first node of the element.

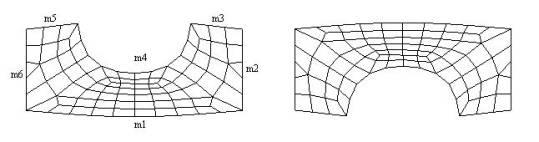
Pattern 162-662

The pattern corresponds to pattern 161-661 with the exception that conditions for subdivision of edges 4 and 5 must be so, that a regular subdivision to quadrilateral elements can be achieved. These conditions are: m5 = m3 and m4 = m1 + m2 + m6 + 2; m5 and m4 are automatically corrected if they do not meet these conditions. Following picture shows pattern 162 and 562.

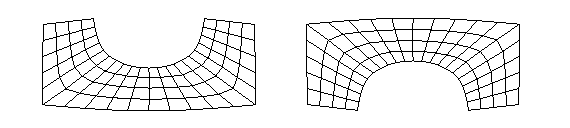
Subdivision of type 400 elements, pattern 150

Macro element type 400 is a planar element with up to 39 edges consisting of straight or circular lines. For subdivision of the element into finite elements, the edge length of the finite elements to be generated must be given using command Division. First the surrounded border of the element is subdivided using this value. Beginning at the borders, quadrilateral and triangular elements are created until the whole area is meshed. If the number of intermediate nodes on all edges is odd, subdivision is done using the double edge length, then all quadrilateral elements are subdivided into 4 and all triangular elements are subdivided into 3 quadrilateral elements; so one gets only quadrilateral elements. This first subdivision with double edge length is only applied, if strongly curved edges have at least 3 intermediate nodes.

Using command Pattern it is also possible to give the number of intermediate nodes for all macro element edges in counter clock wise direction, but the quotient of largest to smallest FE edge length must not be greater than 4. The whole area is meshed using a FE edge length that is equal to the mean value of the length given for all macro element edges.